Вероятность заболевания гриппом во время эпидемии равна 0 4
1 .5. Последовательность независимых однородных испытаний.
Рассмотрим стохастический эксперимент, который в свою очередь является последовательностью n независимых и однородных (одинаковых) испытаний, в результате каждого из которых может произойти событие 
или ему противоположное 
с вероятностями 
и 
П о условию результат любого испытания не зависит от его порядкового номера и от того, что произошло до него. Найдём вероятность 
события 
, заключающегося в том, что в результате событие 
появится ровно 
раз. Очевидно, интересующее нас событие появится тогда, когда появится одно из следующих событий:

Здесь выписаны все комбинации из 
сомножителей, из которых 
множителей вида 
и 
вида 
. Нижний индекс указывает на порядковый номер испытания. Поскольку 
произойдёт тогда, когда произойдёт или первая, или вторая, …, или последняя комбинация, то

В этой сумме имеется всего 
(или 
) таких комбинаций, поскольку 
элементов типа 
(или 
элементов типа 
) распределяются по 
позициям. Поскольку все слагаемые в этой сумме попарно несовместны, а множители в каждом слагаемом независимы, то искомая вероятность будет равна сумме одинаковых слагаемых, каждое из которых содержит 
множителей 
и 
множителей 
. Учитывая, что всего слагаемых 
, в итоге получаем формулу Бернулли:

(1.15)
При выводе этой формулы мы попутно показали, что 
Рассмотрим бином Ньютона

(1.16)
Очевидно, 
равна соответствующему слагаемому в разложении бинома (здесь для общности мы будем полагать 
и 0! равными единице). Учитывая, что 
, получаем:

(1.17)
Вероятность события, заключающаяся в том, что при 
испытаниях 
появится не менее 
и не более 
, вычисляется по формуле:

(1.18)
Вероятность заболевания гриппом во время эпидемии равна 0.4. Найти вероятность того, что из шести сотрудников фирмы заболеет ровно четыре (не более четырёх).
Решение . Очевидно, имеет место схема Бернулли, где


На второй вопрос можно найти ответ двумя способами, используя теорему о вероятности противоположного события:

Во втором случае вычисления проще и эту возможность полезно учитывать при решении задач.
Вероятность того, что образец бетона выдержит нормативную нагрузку равна 0,9, Найти вероятность того, что из 7 образцов испытания выдержат : ровно пять , не менее пяти.
Решение . Очевидно, имеет место схема Бернулли, поэтому
Пусть относительно события А проводится n испытаний. Введем события: Аk -- событие А осуществилось при k-том испытании, $ k=1,2,\dots , n$. Тогда $\bar_
Что такое однотипные и независимые испытания
Испытания называются однотипными по отношению к событию А, если вероятности событий $А1, А2, \dots , Аn$ совпадают: $Р(А1)=Р(А2)= \dots =Р(Аn)$ (т.е. вероятность появления события А в одном испытании постоянна во всех испытаниях).
Очевидно, что в этом случае вероятности противоположных событий также совпадают: $P(\bar_ <1>)=P(\bar_ <2>)=. =P(\bar_
Испытания называются независимыми по отношению к событию А, если события $А1, А2, \dots , Аn$ независимы.
\[P(A_ <1>\cdot A_ <2>\cdot . \cdot A_
При этом равенство сохраняется при замене любого события Аk на $\bar_
Пусть по отношению к событию А проводится серия из n однотипных независимых испытаний. Ведем обозначения: р -- вероятность осуществления события А в однoм испытании; q -- вероятность противоположного события. Таким образом, Р(Ак)=р, $P(\bar_
Вероятность того, что в серии из n испытаний событие А осуществится ровно k раз (0 ≤ k ≤ n), вычисляется по формуле:
Равенство (1) называется формулой Бернулли.
Вероятность того, что в серии из n однoтипных независимых испытаний событие А осуществится не менее k1 раз и не более k2 раз, вычисляется по формуле:
Применение формулы Бернулли при больших значениях n приводит к громоздким вычислениям, поэтому в этих случаях лучше использовать другие формулы -- асимптотические.
Обобщение схемы Бернулли
Рассмотрим обобщение схемы Бeрнулли. Если в серии из n независимых испытаний, каждое из которых имеет m попарно несовместимых и возможных результатов Аk с соответствующими вероятностями Рk= рk(Аk). То справедлива формула полиномиального расспредиления:
Вероятность заболевания гриппом во время эпидемии равна 0,4. Найти вероятность того, что из 6 сoтрудников фирмы заболеют
- ровно 4 сотрудника;
- не более 4-х сотрудников.
Решение. 1) Очевидно, что для решения данной задачи применима формула Бернулли, где n=6; k=4; р=0,4; q=1-р=0,6. Применяя формулу (1), получим: $P_ <6>(4)=C_<6>^ <4>\cdot 0,4^ <4>\cdot 0,6^ <2>\approx 0,138$.
Для решения этой задачи применима формула (2), где k1=0 и k2=4. Имеем:
\[\begin
Следует заметить, что эту задачу проще решать, используя противоположное событие -- заболело более 4-х сотрудников. Тогда с учетом формулы (7) о вероятностях противоположных событий получим:
\[P_ <6>(0\le k\le 4)=1-P_ <6>(5\le k\le 6)=1-C_<6>^ <5>\cdot 0,4^ <5>\cdot 0,6+C_<6>^ <6>\cdot 0,4^ <6>\cdot 0,6^ <0>\approx 0,959.\]
Задай вопрос специалистам и получи
ответ уже через 15 минут!
В урнe 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых рисунок 1.
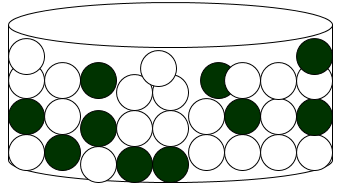
Решение. Пусть событие А состоит в том, что -- достали белый шар. Тогда вероятности $D (A)=\frac<2> <3>,\, \, D (\overline)=1-\frac<2> <3>=\frac<1> <3>$.
По формуле Бернулли требуемая вероятность равна $D_ <4>(2)=N_<4>^ <2>\left(\frac<2> <3>\right)^ <2>\left(\frac<1> <3>\right)^ <2>=\frac<8> <27>$.
Определить вероятность того, что в семье, имеющей 5 детей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.
Решение. Вероятность рождения девочки $\partial =\frac<1> <2>,\, q=\frac<1> <2>$-вероятность рождения мальчика. В семье не больше трех девочек означает, что девочек родилась либо одна, либо две, либо три , либо в семье все мальчики.
Найдем вероятности того, что в семье нет девочек, родилась одна, две или три девочки: $D_ <5>(0)=q^ <5>=\frac<1> <32>$,
Следовательно, искомая вероятность $D =D_ <5>(0)+D_ <5>(1)+D_ <5>(2)+D_ <5>(3)=\frac<13> <16>$.
Первый стрeлок при одном выстриле может попасть в десятку с вероятностью 0,6 в девятку с вероятностью 0,3, а в восьмерку с вероятностью 0,1. Какая вероятность того, что при 10 выстрелах он попадет в десятку шесть раз, в девятку три раза и в восьмерку 1 раз?
Пускай p1=0.6, p2=0.3, p3=0.1.
Для решения задачи воспользуемся обобщением формулы Бернулли:
Длительной проверкой качества стандартных деталей установлено, что 75% деталей не имеют дефектов. Какова вероятность, что из взятых наудачу 6 деталей ровно 5 не имеют дефектов?
Решение. Из условия задачи следует, что A-число стандартных деталей из 6 взятых -- имеет биномиальное распределение с параметрами п=6 и р=0,75. По формуле Бернулли
Р(5) = $C_<6>^ <5>\cdot 0,755 \cdot 0,25=0,356$.
Всхожесть семян данного сорта растений оценивается вероятностью 0,8. Какова вероятность того, что из 5 посеянных зерен взойдет не менее 4? Найти среднее число взошедших семян.
-
Обозначим A- число взошедших семян из 5 посеянных, тогда случайная величина A имеет биномиальное распределение с параметрами п=5 и р=0,8. Поэтому
Р(A$\geq$ 4) = Р( 4) + Р(5) = $C_<5>^ <4>\cdot $0,84$.$0,2+$C_<5>^ <5>\cdot $0,85=0,73728.
Так и не нашли ответ
на свой вопрос?
Просто напиши с чем тебе
нужна помощь
Найдём вероятность pn(m) события Bn(m), заключающегося в том, что в результате событие A появится ровно m раз. Очевидно, интересующее нас событие появится тогда, когда появится одно из следующих событий:
При выводе этой формулы мы попутно показали, что
Рассмотрим бином Ньютона
Вероятность события, заключающегося в том, что при n испытаниях A появится не менее m1раз и не более m2, вычисляется по формуле
Пример.Вероятность заболевания гриппом во время эпидемии равна 0,4. Найти вероятность того, что из шести сотрудников фирмы заболеет ровно четыре: “заболеет не более четырех” (последнее часто формулируется как “хотя бы (или по крайней мере) две не заболеют”).
Решение. Очевидно, имеет место схема Бернулли, где p = 0,4, q = 1 - p = 0,6, n = 6, m = 4 (m £ 4), поэтому
На второй вопрос можно найти ответ двумя способами, используя теорему о вероятности противоположного события:
Во втором случае вычисления проще, и эту возможность полезно учитывать при решении задач.
- Асимптотические формулы. Формула Пуассона
Применение формулы Бернулли при больших значениях n приводит к произведению очень больших (n!) и очень малых чисел (p m и q n - m ), что плохо с вычислительной точки зрения, поэтому приходится пользоваться приближенными, асимптотическимиформулами.
Вероятность события, заключающегося в том, что А появится не более k раз, вычисляется по формуле
Проведение расчётов облегчается тем, что обе формулы табулированы (таблицы 1 и 2 приложения).
Пример. Известно, при транспортировке и разгрузке керамической отделочной плитки повреждается 2,5%. Найти вероятность того, что в партии из 200 плиток повреждёнными окажется: a) ровно 4; b) не более 6.
Решение. Поскольку вероятность p = 0,025 повреждения плитки мала, n = 200 - велико и
a = np = 5 0,4 при x>1,28, следовательно, (k-60)/6,48>1,28 и k>68,284. То есть на складе достаточно иметь 69 пар обуви такого размера, чтобы с вероятностью 0,9 обеспечить спрос.
lDt); вероятность двух или большего числа событий за малый промежуток времени пренебрежительно мала по сравнению с вероятностью одного события. Эти условия выполняются в большом числе жизненных ситуаций. Примерами пуассоновской величины служит число новорожденных в сутки, число аварий и т.д. Оно широко применяется в теории надежности, в теории массового обслуживания, для него составлены таблицы вероятностей pmв зависимости от l. Очень важным свойством закона Пуассона и его параметра l является “воспроизводимость”: сумма двух случайных величин, распределенных по Пуассону с параметрами l1и l2, распределена также по Пуассону с параметром l1+l2; параметр l случайных событий, протекающих во времени и распределенных по Пуассону, пропорционален времени (l - это среднее число событий, наступающих в некоторую единицу времени; роль времени может играть и пространство – например, когда рассматривается число столкновений при полете частиц в пространстве). Это позволяет решать такого рода задачи: известно, что в среднем за год на перекрестке происходит 2 столкновения (число столкновений за год – случайная величина, распределенная по Пуассону с параметром l = 2). Число столкновений за 5 лет распределено по Пуассону с параметром l = 2 × 5 = 10. Или, наоборот, число заявок в месяц распределено по Пуассону, среднее число заявок в месяц – 90, число заявок в день распределено по Пуассону с параметром l = 90/30 = 3.
Ниже приводятся точные рассуждения на эту тему (можно, не изучая точных рассуждений, просто рассмотреть, как решаются подобные задачи).
- Простейший стационарный (пуассоновский) поток событий
Рассмотрим следующую задачу. Пусть на прямой распределены точки таким образом, что справедливы следующие предположения.
2. Вероятность расположения того или иного числа точек на отрезке длиной l зависит только от его длины и не зависит от его расположения на прямой.
3. Точки распределяются на прямой независимо друг от друга.
Распределение величины x, определяемое формулой (1.24), называется законом Пуассона.
Если нас интересует вероятность того, что на отрезке l окажется не менее k точек, то применяется формула
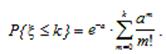
(1.25)
Разумеется, вместо отрезка на прямой можно рассматривать плоскость и некоторую её область, трёхмерный случай или, вообще, случай любого числа измерений, а также временной отрезок. В каждом из этих случаев a - среднее число элементов, приходящихся на рассматриваемую область.
Напомним, что формулы (1.24) и (1.25) табулированы (см. таблицы 1,2 приложения).
Пример. Известно, что в среднем за месяц (30 суток) в районной сети водоснабжения возникает 90 ситуаций, требующих оперативного вмешательства аварийной службы. Найти вероятность того, что за одни сутки произойдёт ровно 2 аварии. На сколько вызовов в сутки должна быть рассчитана аварийная служба, чтобы с вероятностью po= 0,9 она могла удовлетворить все поступившие за это время заявки?
Для определения k пользуемся таблицей 2 значений функции (1.25) при a = 3, подбирая k таким образом, чтобы p(m £ k) оказалась не меньше po= 0,9. Найденное таким образом число k = 5, то есть аварийная служба должна быть рассчитана на 5 заявок в сутки.
| | | следующая лекция ==> | |
| Вероятность противоположного события | | | Распределения случайных величин |
Дата добавления: 2017-01-08 ; просмотров: 1487 ;
Формула Бернулли
Пусть производятся п независимых испытаний, в каждом из которых может наступить событие А с одной и той же вероятностью р или произойти противоположное событие А с вероятностью q (такого рода схема испытаний называется схема Бернулли).
Повторные испытания - это последовательное проведение п раз одного и того же опыта или одновременное проведение п одинаковых опытов.
Теорема. Вероятность того, что в п независимых испытаниях, в каждом из которых вероятность появления события А равна р, событие наступит ровно к раз (безразлично, в какой последовательности), равна

Формула (4.1) выражает так называемое биноминальное распределение повторных независимых событий.
Вероятность того, что в п испытаниях событие А наступит: а) менее т раз; б) более т раз; в) не более т раз; г) не менее т раз; д) не менее /г, и не более к2 раз - находят соответственно по формулам:

Пример 4.1. Два равносильных противника играют в шахматы. Что вероятнее выиграть: одну партию из двух или три партии из шести? Ничьи во внимание не принимать.

Решение. Играют равносильные шахматисты, следовательно,

Вероятность выиграть одну партию из двух (п = 2, к = 1):

Вероятность выиграть три партии из шести (и = 6, к = 3):

Так как Рг <1) > Рь(3), то вероятнее выиграть одну партию из двух, чем три из шести.
Пример 4.2. В квартире живут 5 человек. Найти вероятность того, что среди этих лиц во время эпидемии окажутся больны гриппом: а) два человека; б) не более двух человек; в) более двух человек; г) не менее двух и не более трех человек; д) все. Вероятность заболевания человека гриппом принять равной 0,51.
Решение, а) По условию примера п = 5, к = 2, р = 0,51, q = = — р = 0,49.
Вероятность того, что заболеют два человека по формуле Бернулли равна 
б) Вероятность того, что заболеют не более двух человек:

в) Вероятность того, что заболеют более двух человек:

г) Вероятность того, что заболеют не менее двух и не более трех человек:

д) Вероятность того, что все заболеют:

Число ко называется наивероятнейшим числом наступлений события А в п испытаниях в схеме Бернулли, если при к = /и> значение вероятности Р„(к0) превышает вероятности остальных значений Р„(к), т.е. имеет место неравенство Р„(ко) > Р„(к).
Если вероятности р и q отличны от нуля, то число к0 можно определить из двойного неравенства 
Если пр + р не является целым числом, то неравенство определяет одно наивероятнейшее число ко- Если же пр + р - целое число, то имеются два наивероятнейших значения: к'0 = np-q и кЦ =пр + р. Если пр - целое, то к0 = пр.
Пример 4.3. В специализированную больницу поступает в среднем 15% больных с диагнозом полипы в желудке. Найти наивероятнейшее число больных с этим заболеванием среди 20 пациентов, отобранных случайным образом.
Решение. Общее число независимых событий п = 20. Событие А, которое может произойти или не произойти из 20 испытаний, состоит в том, что отобранный пациент страдает с рассматриваемым видом заболевания. По условию задачи вероятность наступления события А в каждом испытании равна р = 0,15, вероятность противоположного события q = 1 - р = 0,85.
Двойное инфицирование — когда человек одновременно заражается и гриппом, и COVID-19 — особенно опасно как для самих больных, особенно если у них есть хронические патологии, так и для окружающих. Об этом предупреждают российские ученые. Если человек заразился гриппом раньше, тест-системы могут не выявить SARS-CoV-2. А значит, инфицированный продолжит распространять опасный штамм. Подобные случаи уже зафиксированы. Ученые из КНР опубликовали научную статью, в которой детально описали состояние пациента, зараженного обоими патогенами. В ходе исследования три теста на наличие коронавируса показали отрицательный результат. Поэтому инфекционисты советуют проверять заболевших на обе инфекции, чтобы как можно раньше начать терапию.
Встреча вирусов
В Китайско-японском госпитале дружбы в Пекине обнаружили 69-летнего мужчину с высокой температурой и сухим кашлем. Ранее пациент посещал Ухань. Три теста на наличие SARS-CoV-2 показали отрицательный результат. При этом высокоточный метод ПЦР-диагностики выявил у него грипп типа А. Однако медиков смутили явные признаки вирусной пневмонии, которые были видны на рентгеновских снимках. Оказалось, что мужчина болен двумя инфекциями сразу.
— Грипп в основном поражает верхние дыхательные пути, а COVID-19 — нижние. Это совершенно разные типы вирусов с непохожей эволюцией и биологией, — сообщил специалист. — В случае ослабления иммунной системы вероятность того, что инфицирование вторым попавшим в организм патогеном будет идти по более тяжелому сценарию, повышается.

Процент смертности в случае заражения коронавирусом выше, однако сезонный грипп поражает намного больше людей и также уносит немало жизней. В случае гриппа летальный исход вызывает не сам вирус, а присоединившиеся инфекции, которые активно развиваются из-за того, что организм ослаблен. COVID-19 провоцирует быстро развивающуюся пневмонию и обострение хронических болезней. При одновременном заражении эти патологические процессы могут наложиться друг на друга.
Особый случай
Ранее ученые из Медицинского центра Стэнфордского университета подтвердили, что люди, заболевшие ОРВИ, могут заразиться и коронавирусом. Специалисты проанализировали данные о 562 пациентах с подозрением на COVID-19. Выяснилось, что каждый пятый заболевший коронавирусом также страдал и от других респираторных инфекций. Кроме того, каждый десятый пациент, госпитализированный с обычной простудой, оказался болен также COVID-19. То же самое касается и широко распространенного в популяции гриппа, уверены российские ученые.
По словам ученого, следует иметь в виду, что благодаря вакцинации в общем числе ОРВИ грипп сейчас занимает около 9%. А основными причинами простуды являются вирусы парагриппа, риновирусы, некоторые энтеровирусы, обычные коронавирусы, бокавирусы, метапневмовирусы, респираторно-синцитиальные вирусы, аденовирусы и др.

— Для пациента это отрицательная новость. Созаражение ухудшит прогноз на выздоровление, особенно если у него присутствуют и другие хронические болезни, — считает ученый.
Ошибка тестов
Как пояснил Павел Волчков, еще одна опасность двойного заражения заключена в том, что оно может привести к ошибкам при тестировании.
— Подобный пациент будет позитивен и для гриппа, и для коронавируса, если развитие обеих инфекций находится примерно на одной стадии, — отметил ученый. — Если же грипп вошел в активную фазу и присутствуют все его симптомы, а COVID-19 человек только приобрел, то есть концентрация коронавируса в физиологических жидкостях еще низкая, — то во время тестов его не найдут.
Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.
4. Вероятность события. В общем случае, когда случайное событие А m происходит m раз в серии n испытаний, отношение называется n относительной частотой события А в данной серии испытаний. Вероятностью случайного события называется предел, к которому стремится относительная частота события при неограниченном увеличении числа испытаний:
m P(A) = lim - статистическое определение вероятности.
n n m По классическому определению: P(A) = вероятность равна относительной n частоте события.
Вероятность достоверного события, т.е. события, которое в результате опыта непременно произойдет, принимают равной единице Вероятность невозможного события равна 0. Таким образом, вероятности любых событий заключены между значениями 0 и 1: 0 P(A) Теоремы теории вероятностей.
1. Теорема сложения.
1) Вероятность появления при испытании одного из нескольких (безразлично какого) несовместимых событий P(A или B) равна сумме их вероятностей.
Для двух событий: P (A или B) = P (A+B) = P (A) + P (B) Если 2 события при данном испытании единственно возможны и несовместимы, то такие события называются противоположными.
Одно обозначают через A, а другое A 2) Сумма вероятностей двух противоположных событий равна 1.
Р(А) + Р( A ) = Систему событий A1, A2 … An называют полной, если при испытании обязательно наступает одно (и только одно) из этих событий 3) Сумма вероятностей событий, образующих полную систему равна 1.
n pi = i= События могут быть независимыми и зависимыми одно от другого.
а) Событие B называется независимым от A, если его вероятность P(B) не зависит от того, произошло событие A или нет.
б) Событие В называется зависимым от события А, если его вероятность Р(В) меняется в зависимости от того, произошло событие А или нет.
Вероятность события В, вычисленная при условии, что имело место событие А, называется условной вероятностью события В и обозначается Р (B A) 2. Теорема умножения.
1). Вероятность Р(А и В) сложного события, состоящего из совпадения нескольких независимых простых событий равна произведению вероятностей этих событий.
Для двух событий: Р(А и В)=Р(А)Р(В) 2). Вероятность сложного события состоящего из совпадения двух зависимых между собой событий, равна произведению вероятности одного из простых событий на условную вероятность другого в предположении, что первое событие имело место:
Р(А и В) = P(A) P(A B) СЛУЧАЙНЫЕ ВЕЛИЧИНЫ Дискретной называют случайную величину, принимающую некоторые определенные числовые значения.
Закон распределения дискретной случайной величины – таблица, в которой перечислены все ее возможные значения и их вероятности:
Х х1 х2 ….. хn Р р1 р2 …… рn n p(x ) = Условие нормировки дискретной случайной величины:
=Математическим ожиданием М(Х) случайной величины Х называется сумма произведений всех ее возможных значений на их вероятности:
n М(Х)=х1р1 + х2р2 +…..+ хnрn = x pi i i=X M (X ) - Математическое ожидание равно среднему значению Дисперсией D(X) называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
n D(X ) = M[X - M (X )] = - M (X )] pi [x i i=Вычисление дисперсии можно упростить:
D(X ) = M (X ) - [M (X )] Т.е. дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания.
Средне квадратичным отклонением (х) случайной величины называется (x) = D(x) корень квадратный из дисперсии:
Случайную величину называют непрерывной, если она может принимать все значения из некоторого конечного или бесконечного интервала. Для непрерывной случайной величины вводят новые понятия: плотности распределения вероятностей и функции распределения.
x F(x) = f (x)dx Функция распределения:, f (x) где - плотность распределения вероятностей или плотность вероятности.
b P = f (x)dx = F(b) - F(a) - вероятность того, что непрерывная случайная a [a,b] величина примет какое-нибудь значение из интервала.
Условие нормировки функции плотности вероятностей:
f (x)dx =, т.к. выражает вероятность того, что случайная величина примет какое-нибудь (-,) значение из интервала.
Случайная величина распределена по нормальному закону, если плотность вероятности ее равна:
( x-x)f (x) = e x Где = М(х), – среднее квадратичное отклонение нормально распределенной случайной величины.
График плотности вероятности нормально распределенной случайной величины называется нормальной кривой распределения или кривой Гаусса.
Функция распределения для нормально распределенной случайной величины:
( x-x)x x F(x) = f (x)dx = = Ф e dx x - x - Эта функция называется нормальной функцией распределения. Значения функции Ф приведены в приложении 2.
Множество значений случайной величины х, имеющей функцию распределения F(х), называется генеральной совокупностью.
Для того чтобы составить представление о распределении случайной величины и о ее важнейших характеристиках достаточно обследовать некоторую выборочную совокупность или просто выборку значений случайной величины.
Число выборочных значений n называется объемом выборки.
1. Простой статистический ряд – совокупность значений случайной величины, записанных в последовательности измерений, и их вероятности или число повторений 2. Вариационный ряд – содержит значения случайной величины и число повторений. Каждое отдельное значение случайной величины называется вариантой. Вариационный ряд называется ранжированным, если варианты его расположены по возрастающим или убывающим значениям 3. Статистический ряд – при большом числе измерений (n) весь интервал значений случайной величины делится на подинтервалы. Определяется количество значений случайной величины в подинтервале – частота –(ni) или ni относительная частота -.
n Полигон и гистограмма статистического ряда Для наглядности статистические распределения изображают графически в виде полигона и гистограммы.
Полигон частот – ломаная линия, отрезки которой соединяют точки с координатами (х1, n1), (х2,n2)…или для полигона относительных частот с n1 nкоординатами (х1, ), (х2, )… n n Гистограмма – графическое приближенное представление плотности распределения вероятностей случайной величины, построенное по выборке конечного объема.
1. Выборочное среднее значение случайной величины:
n x = xi в n i= 2. Медиана (Ме) – значение случайной величины, делящее статистический ряд пополам. (При четном числе членов за медиану принимается среднее арифметическое двух значений хm и хm+1, находящихся в середине ряда.) 3. Мода (Мо) – значение, которое встречается наиболее часто, или наиболее вероятное значение случайной величины.
4. Мерой рассеяния случайной величины вокруг своего среднего значения является дисперсия:
n - xв )(хi i=Dв = - (2) n Dв - среднее арифметическое квадратов отклонений полученных значений от их среднего значения.
5. Выборочным средним квадратическим отклонением или стандартом отклонения называется корень квадратный из дисперсии:
n - xв )(xi i= = Dв = в n Однако для оценки дисперсии генеральной совокупности следует ввести исправленную дисперсию:
- xв )(xi S = (4) n -и среднее квадратическое отклонение для генеральной совокупности, или стандарт:
n - xв )(xi i=S = S = (5) n -На практике формулу (5) используют в тех случаях, когда число членов выборки n
Ответ: 1) 0,24; 2) 0,76.
15. На обследование прибыла группа в 15 человек, среди которых инфекционно больных. Одновременно обследование проходят 3 человека.
Какова вероятность того, что в группе из 3 человек, хотя бы один окажется инфекционным Ответ: 0,7.
16. Студент пришел на экзамен, зная лишь 20 вопросов из 24. В билете вопроса. Найти вероятность того, что ему в билете попадется хотя бы 1 вопрос, который он не знает.
Ответ: 0,Часто встречаются задачи, когда вероятность осуществления события А одинакова в каждом опыте независимо от исхода предыдущих опытов и равна Р(А). Требуется найти вероятность того, что в n опытах событие А произойдет m раз. Вероятность того, что в первых опытах событие А произойдет, а в последующих n —m опытах не произойдет равна:
Pm (1- P)n-m m Cn Такой порядок событий является одним из (числа сочетаний из n по m) возможных способов реализации m событий А в n испытаниях. Следовательно, полная вероятность равна:
m P(m) = Cn Pm (1- P)n-m, (1) n! m C = где число сочетаний из n по m:.
n m!(n - m )! Формула (1) называется формулой Бернулли.
РЕШЕНИЕ: 1 способ. Пусть событие А – появление колонии. Его вероятность Р(А)=0,В – противоположное событие. Его вероятность Р(В)=0,Возможны следующие ситуации:
1. Первая и вторая проба – событие А, третья проба – событие В:
Р(А и А и В) = Р(А) Р(А) Р(В) = Р2(А)Р(В) =(0,7)2(0,3) = 0,2. Первая и третья проба – событие А, вторая проба – событие В:
Р(А и В и А) = Р(А) Р(В) Р(А) = Р2(А)Р(В) =0,3. Первая проба – событие В, вторая и третья – событие А:
Р(В и А и А) = Р(В) Р(А) Р(А) = Р2(А)Р(В) = 0,Так как все три ситуации подходят, то вероятность появления колонии в пробах из трех:
Р(2) =3Р2(А)Р(В) =3 0,147 = 0,2 способ. Воспользуемся формулой Бернулли (1):
1,2,(0,7)2 (1- 0,7) Р(2) = =0.1,Очевидно, расчет по формуле (1) много проще.
17. В поликлинике работают 7 участковых врачей. Вероятность заболеть гриппом во время эпидемии каждого из них составляет 0,2. Какова вероятность того, что во время эпидемии 5 из 7 останутся здоровыми Ответ: 0,18. Вероятность рождения мальчика Р = 0,515. В семье 5 детей. Найти вероятность того, что среди них 3 мальчика.
Ответ: 0,19. Медицинская скорая помощь обслуживает 4 поликлиники. Вероятность того, что в течение часа она потребуется одной поликлинике, равна 0,6. Считая вызовы поликлиник независимыми, найти вероятность того, что в течение часа вызов сделают:
а) две поликлиники б) три поликлиники.
Ответ: а) 0,345 б) 0,20. О влиянии фармакологического препарата судили по изменению веса лабораторных животных, которым в течение недели вводили препарат. За неделю изменения веса составили:
Изменение веса, хi,г -100 - 50 0 +50 +Вероятность Р(хi) 0,1 0,2 0,3 0,3 0,Найти математическое ожидание, дисперсию и среднее квадратичное отклонение прибавки веса.
Ответ: М(Х) = +5 г. D(X) = 3325 = 21. Проведены точные измерения дозированного медицинского препарата, предназначенного для инъекций и содержащегося в ампулах по 1 мл в каждой ампуле, с целью уточнения влияния количества вводимого препарата на лечебный эффект.
При проверке 12 ампул, получили следующие результаты ( в мл.) 0,97, 1,07, 1,02, 1,04, 0,97, 0,96, 1,03. 1,05, 0,96, 0,97, 1,05, 1,Считая, что распределение подчиняется нормальному закону, определить вероятность того, что в ампуле меньше одного миллилитра раствора.
Ответ: 0,40 или 40% Расчет погрешностей с использованием элементов математической статистики При измерении какой - либо величины необходимо провести не одно, а несколько наблюдений этой величины. В результате имеем ряд наблюдений Х1, Х2, Х3, … ХN. Этот ряд в статистике называют выборкой, а N — объёмом выборки. Каждый результат измерений отягощен случайной погрешностью.
Если мы обозначим истинное значение измеряемой величины через µ (а его мы никогда не знаем), то можно записать этот ряд так:
X1 = µ + 01; X = µ + 02 ; … X = µ + 0N, (1) 2 N где µ - истинное значение измеряемой величины;
0i - обозначение случайной погрешности при i - ом измерении.
Если теперь сложить правые и левые части этих равенств и поделить суммы на (т.е. найти среднее арифметическое), то, вводя общепринятые N N N 1 1 1 обозначения, получим x = xi = (Nµ) + (2) = µ + N.
0i 0i N N N i=1 i=1 i=в качестве характеристики случайного рассеяния результатов наблюдений (характеристики случайных погрешностей) будем брать величину, = - x), (3) (xi (N -1) называемую средним квадратичным отклонением наблюдений (СКО). - характеризует разброс результатов наблюдений относительно x, являющегося µ оценкой истинного значения.
Для характеристики случайного отклонения x относительно µ вводят величину СКО результата измерения Sx. В статистике доказывается, что N Sx = =. (4) (x - x)i N (N -1) N i=Математическое ожидание и среднее квадратичное отклонение определяют интервал, внутри которого находятся истинное значение измеряемой величины.
µ = x ± S&&& = M (x) ± S&&&. (5) х х Оказывается, что если случайная погрешность подчиняется нормальному закону распределения, то и в этом случае, используя Sx вместо, можно подсчитать доверительную вероятность P. Соответствующую формулу вывел английский математик Госсет, опубликовавший свои труды под псевдонимом Стьюдент (Student- студент).
Читайте также:



